最短路径

Dijkstra 算法

基于贪心的单源最短路算法，其要求图中的边全部非负。

算法描述

procedure Dijkstra(G：边全为正权的图） 2 {G带有顶点 $a=v_{0},v_{1},v_{2}…$}和若干边 $w(v_{i},v_{j})$ 3 for i:=1 to n 4 $D(v_{i}):=\infty $ 5 D(a):=0 6 $S:=\emptyset$ 7 while $z\notin S$ 8 begin 9 u:=不属于S的D(u)最小的一个顶点 10 $S:=S\cup {u}$ 11 for 所有不属于S的顶点v 12 if D(u)+w(u,v)<D(v) then D(v):=D(u)+w(u,v) 13 end{D(z)=从a到z的最短路长度}

使用优先队列

1 function Dijkstra(G, w, s) 2 INITIALIZE-SINGLE-SOURCE(G, s) //实际上的操作是将每个除原点外的顶点的d[v]置为无穷大，d[s]=0 3 $S\leftarrow \emptyset$ 4 $Q\leftarrow s$ // Q是顶点V的一个优先队列，以顶点的最短路径估计排序 5 while( $Q\not =\emptyset $) 6 do $u\leftarrow EXTRACT-MIN(Q)$ //选取u为Q中最短路径估计最小的顶点 7 $S\leftarrow S\cup u$ 8 for each vertex $v \in Adj[u]$ 9 do RELAX(u, v, w) //松弛成功的结点会被加入到队列中

http://codeforces.com/blog/entry/16221 :

Pseudo code :

dijkstra(v) :
        d[i] = inf for each vertex i
        d[v] = 0
        s = new empty set
        while s.size() < n
                x = inf
                u = -1
                for each i in V-s //V is the set of vertices
                        if x >= d[i]
                                then x = d[i], u = i
                insert u into s
                // The process from now is called Relaxing
                for each i in adj[u]
                        d[i] = min(d[i], d[u] + w(u,i))

int mark[MAXN];
void dijkstra(int v){
	fill(d,d + n, inf);
	fill(mark, mark + n, false);
	d[v] = 0;
	int u;
	while(true){
		int x = inf;
		u = -1;
		for(int i = 0;i < n;i ++)
			if(!mark[i] and x >= d[i])
				x = d[i], u = i;
		if(u == -1)	break;
		mark[u] = true;
		for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
			if(d[p.first] > d[u] + p.second)
				d[p.first] = d[u] + p.second;
	}
}

Two)

Using std :: set :

void dijkstra(int v){
	fill(d,d + n, inf);
	d[v] = 0;
	int u;
	set<pair<int,int> > s;
	s.insert({d[v], v});
	while(!s.empty()){
		u = s.begin() -> second;
		s.erase(s.begin());
		for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
			if(d[p.first] > d[u] + p.second){
				s.erase({d[p.first], p.first});
				d[p.first] = d[u] + p.second;
				s.insert({d[p.first], p.first});
			}
	}
}

Using std :: priority_queue (better):

bool mark[MAXN];
void dijkstra(int v){
	fill(d,d + n, inf);
	fill(mark, mark + n, false);
	d[v] = 0;
	int u;
	priority_queue<pair<int,int>,vector<pair<int,int> >, greater<pair<int,int> > > pq;
	pq.push({d[v], v});
	while(!pq.empty()){
		u = pq.top().second;
		pq.pop();
		if(mark[u])
			continue;
		mark[u] = true;
		for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
			if(d[p.first] > d[u] + p.second){
				d[p.first] = d[u] + p.second;
				pq.push({d[p.first], p.first});
			}
	}
}

Problem: ShortestPath Query

Implement 1

// A C++ program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
#include <iostream>
using namespace std;
#include <limits.h>

// Number of vertices in the graph
#define V 9

// A utility function to find the vertex with minimum distance value, from
// the set of vertices not yet included in shortest path tree
int minDistance(int dist[], bool sptSet[])
{

	// Initialize min value
	int min = INT_MAX, min_index;

	for (int v = 0; v < V; v++)
		if (sptSet[v] == false && dist[v] <= min)
			min = dist[v], min_index = v;

	return min_index;
}

// A utility function to print the constructed distance array
void printSolution(int dist[])
{
	cout <<"Vertex \t Distance from Source" << endl;
	for (int i = 0; i < V; i++)
		cout << i << " \t\t"<<dist[i]<< endl;
}

// Function that implements Dijkstra's single source shortest path algorithm
// for a graph represented using adjacency matrix representation
void dijkstra(int graph[V][V], int src)
{
	int dist[V]; // The output array. dist[i] will hold the shortest
	// distance from src to i

	bool sptSet[V]; // sptSet[i] will be true if vertex i is included in shortest
	// path tree or shortest distance from src to i is finalized

	// Initialize all distances as INFINITE and stpSet[] as false
	for (int i = 0; i < V; i++)
		dist[i] = INT_MAX, sptSet[i] = false;

	// Distance of source vertex from itself is always 0
	dist[src] = 0;

	// Find shortest path for all vertices
	for (int count = 0; count < V - 1; count++) {
		// Pick the minimum distance vertex from the set of vertices not
		// yet processed. u is always equal to src in the first iteration.
		int u = minDistance(dist, sptSet);

		// Mark the picked vertex as processed
		sptSet[u] = true;

		// Update dist value of the adjacent vertices of the picked vertex.
		for (int v = 0; v < V; v++)

			// Update dist[v] only if is not in sptSet, there is an edge from
			// u to v, and total weight of path from src to v through u is
			// smaller than current value of dist[v]
			if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX
				&& dist[u] + graph[u][v] < dist[v])
				dist[v] = dist[u] + graph[u][v];
	}

	// print the constructed distance array
	printSolution(dist);
}

// driver program to test above function
int main()
{

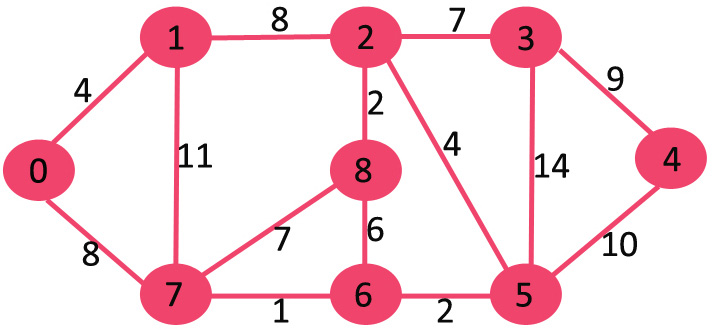
	/* Let us create the example graph discussed above */
	int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
						{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
						{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
						{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
						{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
						{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
						{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
						{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
						{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };

	dijkstra(graph, 0);

	return 0;
}

// This code is contributed by shivanisinghss2110

Implement 2: priority_queue

priority_queue 模板有 3 个参数，其中两个有默认的参数；第一个参数是存储对象的类型，第二个参数是存储元素的底层容器，第三个参数是函数对象，它定义了一个用来决定元素顺序的断言。因此模板类型是：

template <typename T, typename Container=std::vector<T>, typename Compare=std::less<T>> class priority_queue

如你所见，priority_queue 实例默认有一个 vector 容器。函数对象类型 less 是一个默认的排序断言，定义在头文件 function 中，决定了容器中最大的元素会排在队列前面。fonction 中定义了 greater，用来作为模板的最后一个参数对元素排序，最小元素会排在队列前面。当然，如果指定模板的最巵一个参数，就必须提供另外的两个模板类型参数。

#include<bits/stdc++.h> 
using namespace std; 
# define INF 0x3f3f3f3f 
  
// iPair ==> Integer Pair（整数对）
typedef pair<int, int> iPair; 
  
// 加边
void addEdge(vector <pair<int, int> > adj[], int u, 
                                     int v, int wt) 
{ 
    adj[u].push_back(make_pair(v, wt)); 
    adj[v].push_back(make_pair(u, wt)); 
} 
   
  
// 计算最短路
void shortestPath(vector<pair<int,int> > adj[], int V, int src) 
{ 
    // 关于stl中的优先队列如何实现，参考下方网址：
    // http://geeksquiz.com/implement-min-heap-using-stl/ 
    priority_queue< iPair, vector <iPair> , greater<iPair> > pq; 
  
    // 距离置为正无穷大
    vector<int> dist(V, INF); 
    vector<bool> visited(V, false);

    // 插入源点，距离为0
    pq.push(make_pair(0, src)); 
    dist[src] = 0; 
  
    /* 循环直到优先队列为空 */
    while (!pq.empty()) 
    { 
        // 每次从优先队列中取出顶点事实上是这一轮最短路径权值确定的点
        int u = pq.top().second; 
        pq.pop(); 
        if (visited[u]) {
            continue;
        }
        visited[u] = true;
        // 遍历所有边
        for (auto x : adj[u]) 
        { 
            // 得到顶点边号以及边权
            int v = x.first; 
            int weight = x.second; 
  
            //可以松弛
            if (dist[v] > dist[u] + weight) 
            { 
                // 松弛 
                dist[v] = dist[u] + weight; 
                pq.push(make_pair(dist[v], v)); 
            } 
        } 
    } 
  
    // 打印最短路
    printf("Vertex Distance from Source\n"); 
    for (int i = 0; i < V; ++i) 
        printf("%d \t\t %d\n", i, dist[i]); 
} 
int main() 
{ 
    int V = 9; 
    vector<iPair > adj[V]; 
    addEdge(adj, 0, 1, 4); 
    addEdge(adj, 0, 7, 8); 
    addEdge(adj, 1, 2, 8); 
    addEdge(adj, 1, 7, 11); 
    addEdge(adj, 2, 3, 7); 
    addEdge(adj, 2, 8, 2); 
    addEdge(adj, 2, 5, 4); 
    addEdge(adj, 3, 4, 9); 
    addEdge(adj, 3, 5, 14); 
    addEdge(adj, 4, 5, 10); 
    addEdge(adj, 5, 6, 2); 
    addEdge(adj, 6, 7, 1); 
    addEdge(adj, 6, 8, 6); 
    addEdge(adj, 7, 8, 7); 
  
    shortestPath(adj, V, 0); 
  
    return 0; 
}

P4779 单源最短路径

给定一个 n 个点，m 条有向边的带非负权图，请你计算从 s 出发，到每个点的距离。

数据保证你能从 s 出发到任意点。

Floyd

是一种基于动态规划的多源最短路算法

Floyd-Warshal()
	d[v][u] = inf for each pair (v,u)
	d[v][v] = 0 for each vertex v
	for k = 1 to n
		for i = 1 to n
			for j = 1 to n
				d[i][j] = min(d[i][j], d[i][k] + d[k][j])

Time complexity : O(n3).

Bellman-Ford

不仅可以处理负权边，还能处理负环

对所有的点进行V-1次松弛操作,理论上就找到了从源点到其他所有点的最短路径.

如果还可以继续松弛, 说明原图中有环.

其优于迪科斯彻算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达O(|V||E|)

贝尔曼-福特算法简单地对所有边进行松弛操作，共|V|-1次，其中|V|是图的点的数量

procedure BellmanFord(list vertices, list edges, vertex source)
   // 讀入邊和節點的列表並對distance和predecessor寫入最短路徑

   // 初始化圖
   for each vertex v in vertices:
       if v is source then distance[v] := 0
       else distance[v] := infinity
       predecessor[v] := null

   // 對每一條邊重複操作
   for i from 1 to size(vertices)-1:
       for each edge (u, v) with weight w in edges:
           if distance[u] + w < distance[v]:
               distance[v] := distance[u] + w
               predecessor[v] := u

   // 檢查是否有負權重的回路
   for each edge (u, v) with weight w in edges:
       if distance[u] + w < distance[v]:
           error "圖包含負權重的回路"

http://codeforces.com/blog/entry/16221 :

Bellman-Ford(int v)
	d[i] = inf for each vertex i
	d[v] = 0
	for step = 1 to n
		for all edges like e
			i = e.first // first end
			j = e.second // second end
			w = e.weight
			if d[j] > d[i] + w
				if step == n
					then return "Negative cycle found"
				d[j] = d[i] + w

Time complexity : O(nm).

SPFA (Shortest Path Faster Algorithm)

https://zh.wikipedia.org/wiki/%E6%9C%80%E7%9F%AD%E8%B7%AF%E5%BE%84%E5%BF%AB%E9%80%9F%E7%AE%97%E6%B3%95

国际上一般认为是队列优化的Bellman-Ford 算法

这里的 $Q$ 是一个备选节点的先进先出队列， $w(u,v)$ 是边 $(u,v)$ 的权值。

 procedure Shortest-Path-Faster-Algorithm(G, s)
      for each vertex v ≠ s in V(G)
          d(v) := ∞
      d(s) := 0
      offer s into Q
      while Q is not empty
          u := poll Q
          for each edge (u, v) in E(G)
              if d(u) + w(u, v) < d(v) then
                  d(v) := d(u) + w(u, v)
                  if v is not in Q then
                      offer v into Q

http://codeforces.com/blog/entry/16221 :

SPFA(v):
	d[i] = inf for each vertex i
	d[v] = 0
	queue q
	q.push(v)
	while q is not empty
		u = q.front()
		q.pop()
		for each i in adj[u]
			if d[i] > d[u] + w(u,i)
				then d[i] = d[u] + w(u,i)
				if i is not in q
					then q.push(i)

算法-最短路径

最短路径

Dijkstra 算法

算法描述

Implement 1

Implement 2: priority_queue

P4779 单源最短路径

Floyd

Bellman-Ford

SPFA (Shortest Path Faster Algorithm)

References