机器人位姿描述

Objective

  • 绘制世界坐标系
  • 如何描述机器人的位姿
  • 如何绘制世界坐标系
  • 如何绘制机器人位姿

可参考：3.2.2 ロボットの姿勢と描く

対向２輪ロボット(Differential wheeled robot)

robot_vels

机器人位姿

  • 世界坐标系记为 $\Sigma_{world}$

  • 位姿 (状态)：位置和朝向 $x = (x, y, \theta)^T$

  • 状态空间： 姿势（状态）的集合

位姿x所有可能的取值的集合$\chi$，例如平面上的长方形的范围内自由移动的机器人位姿的状态空间为：

$$ \chi = { x=(x, y, \theta)^T | x \in [x_{min}, x_{max}], y \in [y_{min}, y_{max}], \theta \in [- \pi, \pi) } $$

Source Code

import matplotlib.pyplot as plt
import matplotlib.patches as patches
import math
import numpy as np

class World:
  def __init__(self):
    self.objects = []

  def append(self, obj):
    self.objects.append(obj)
  
  def draw(self):
    fig = plt.figure(figsize=(8, 8))
    ax = fig.add_subplot(111)
    ax.set_aspect('equal')
    ax.set_xlim(-5, 5)
    ax.set_ylim(-5, 5)
    ax.set_xlabel("X", fontsize=20)
    ax.set_ylabel("Y", fontsize=20)

    for obj in self.objects:
      obj.draw(ax)
      
    plt.show()

class IdealRobot:
  def __init__(self, pose, color="black"):
    self.pose = pose //位姿
    self.r = 0.2 // 半径
    self.color = color // 顡色

  def draw(self, ax):
    x, y, theta = self.pose
    xn = x + self.r * math.cos(theta)
    yn = y + self.r * math.sin(theta)
    ax.plot([x, xn], [y, yn], color=self.color)
    c = patches.Circle(xy=(x,y), radius=self.r, fill=False, color=self.color)
    ax.add_patch(c)

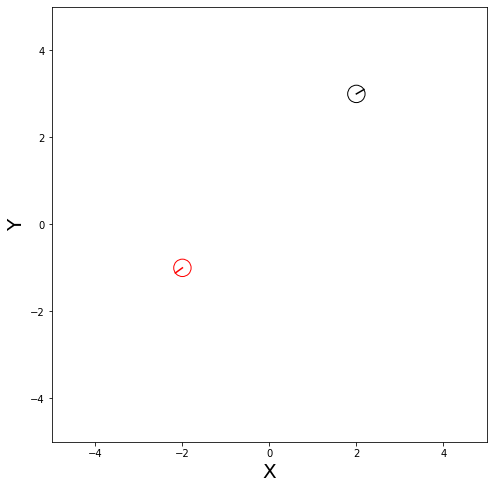
world = World()

robot1 = IdealRobot(np.array([2, 3, math.pi/6]).T)
robot2 = IdealRobot(np.array([-2, -1, math.pi/5*6]).T, "red")
world.append(robot1)
world.append(robot2)

world.draw()

References

comments powered by Disqus