运动方程

内容

  • 运动方程，
  • 控制命令，
  • 让机器人动起来。

robot_moving_demo

理论

robot motion1

(Refered From: https://github.com/ryuichiueda/LNPR_SLIDES/blob/master/old_version/figs/robot_motion1.png)

robot motion2 (Refered From: https://github.com/ryuichiueda/LNPR_SLIDES/raw/master/old_version/figs/robot_motion2.png)

相关变量

  • 速度: $nv [m/s]$
  • 角速度： $\omega [rad/s]$
  • 制御指令：从 $t-1$ 时刻到$t$时刻的运动指令 $u_t = (\nu_t, \omega_t)$ 　

制御指令（せいぎょしれい）は離散時刻ごとにしか変えられないことにします。時刻$t-1$からt までの制御指令を$u_t = (\nu_t, \omega_t)$ と表記します。

u 是相对于机器人的，那么其在世界坐标系下的速度应该如何表示。

$$ \begin{pmatrix} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{pmatrix} = \begin{pmatrix} \nu\cos\theta \\ \nu\sin\theta \\ \omega \end{pmatrix} $$

从t-1时刻到t时刻的角度变化：

$$ \theta_t = \theta_{t-1} + \int_{0}^{\delta t} \omega_t dt = \theta_{t-1} + \omega_t \Delta t $$

从t-1时刻到t时刻的位置的变化方程为：

$$ \begin{pmatrix} x_t \\ y_t \end{pmatrix} = \begin{pmatrix} x_{t-1} \\ y_{t-1} \end{pmatrix} + \begin{pmatrix} \int_{0}^{\Delta t}\nu_t cos(\theta_{t-1} + \omega t) dt \\ \int_{0}^{\Delta t}\nu_t sin(\theta_{t-1} + \omega t) dt \end{pmatrix} $$

机器人的运动方程：(P70)

if $\omega_t == 0$:

$$ \begin{pmatrix} x_t \\ y_t \\ \theta_t \end{pmatrix} = \begin{pmatrix} x_{t-1} \\ y_{t-1} \\ \theta_{t-1} \end{pmatrix} + \begin{pmatrix} \nu_t \cos \theta_{t-1} \\ \nu_t \sin \theta_{t-1} \\ \omega_t \end{pmatrix} \Delta t $$

else:

$$ \begin{pmatrix} x_t \\ y_t \\ \theta_t \end{pmatrix} = \begin{pmatrix} x_{t-1} \\ y_{t-1} \\ \theta_{t-1} \end{pmatrix} + \begin{pmatrix} \nu_t \omega_t^{-1} {\sin( \theta_{t-1} + \omega_t \Delta t ) - \sin \theta_{t-1} } \\ \nu_t \omega_t^{-1} {-\cos( \theta_{t-1} + \omega_t \Delta t ) + \cos \theta_{t-1} } \\ \omega_t \Delta t \end{pmatrix} $$

状態遷移関数

$$ x_t = f(x_{t-1}, u_t), (t= 1,2, 3,…) $$

Example

%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import math
import numpy as np

# Animation
import matplotlib
matplotlib.use('nbagg')
import matplotlib.animation as anm
from matplotlib import rc

%matplotlib inline
class World:
  def __init__(self, debug=False):
    self.objects = []
    self.debug = debug

  def append(self, obj):
    self.objects.append(obj)
  
  def draw(self):
    global ani
    fig = plt.figure(figsize=(4, 4))
    plt.close()
    ax = fig.add_subplot(111)
    ax.set_aspect('equal')
    ax.set_xlim(-5, 5)
    ax.set_ylim(-5, 5)
    ax.set_xlabel("X", fontsize=20)
    ax.set_ylabel("Y", fontsize=20)

    elems = []


    if self.debug:
      for i in range(1000):
        self.one_step(i, elems, ax)
    else:
      ani = anm.FuncAnimation(fig, self.one_step, fargs=(elems, ax), frames=10, interval=1000, repeat=False )
      plt.show()


  def one_step(self, i, elems, ax):
    while elems: elems.pop().remove()
    elems.append(ax.text(-4.4, 4.5, "t="+str(i), fontsize=10) )
    for obj in self.objects:
      obj.state_transition(1, 0.0, 1.0)
      obj.draw(ax, elems)
    
class IdealRobot:
  def __init__(self, pose, color="black"):
    self.pose = pose
    self.r = 0.2
    self.color = color

  def draw(self, ax, elems):
    x, y, theta = self.pose
    xn = x + self.r * math.cos(theta)
    yn = y + self.r * math.sin(theta)
    elems += ax.plot([x, xn], [y, yn], color=self.color)
    c = patches.Circle(xy=(x,y), radius=self.r, fill=False, color=self.color)
    elems.append(ax.add_patch(c))

  def state_transition(self, v_t, w_t, delta_t):
    theta_t_pre = self.pose[2]
    if math.fabs(w_t) < 1e-10:
      self.pose += np.array([v_t * math.cos(theta_t_pre),
                                  v_t * math.sin(theta_t_pre),
                                  w_t
      ]) * delta_t
    else:
      self.pose += np.array([  v_t/w_t * (math.sin(theta_t_pre + w_t * delta_t) - math.sin(theta_t_pre)),
                              v_t/w_t * (-math.cos(theta_t_pre + w_t * delta_t) + math.cos(theta_t_pre)),
                              w_t * delta_t
      ])


%matplotlib inline
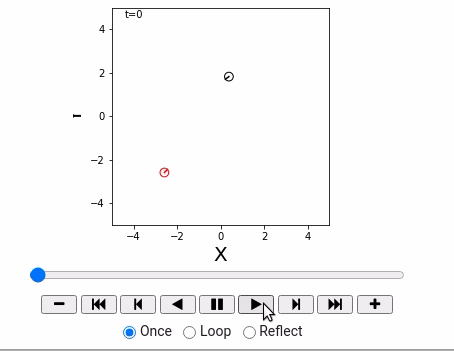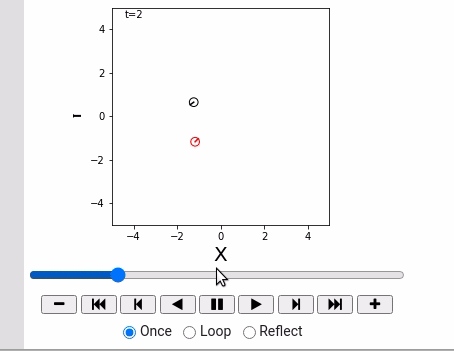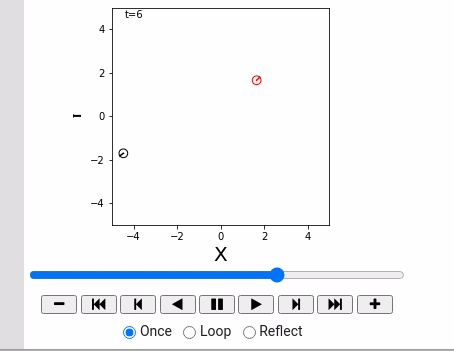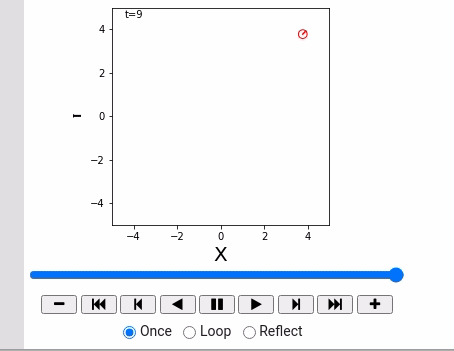
world = World(debug=False)

robot1 = IdealRobot(np.array([2, 3, math.pi/5*6]).T)
robot2 = IdealRobot(np.array([-4, -4, math.pi/4]).T, "red")
world.append(robot1)
world.append(robot2)

world.draw()

# this is needed to show animation whithin colab
rc('animation', html='jshtml')
ani    # or HTML(anim.to_jshtml()
comments powered by Disqus