观测方程
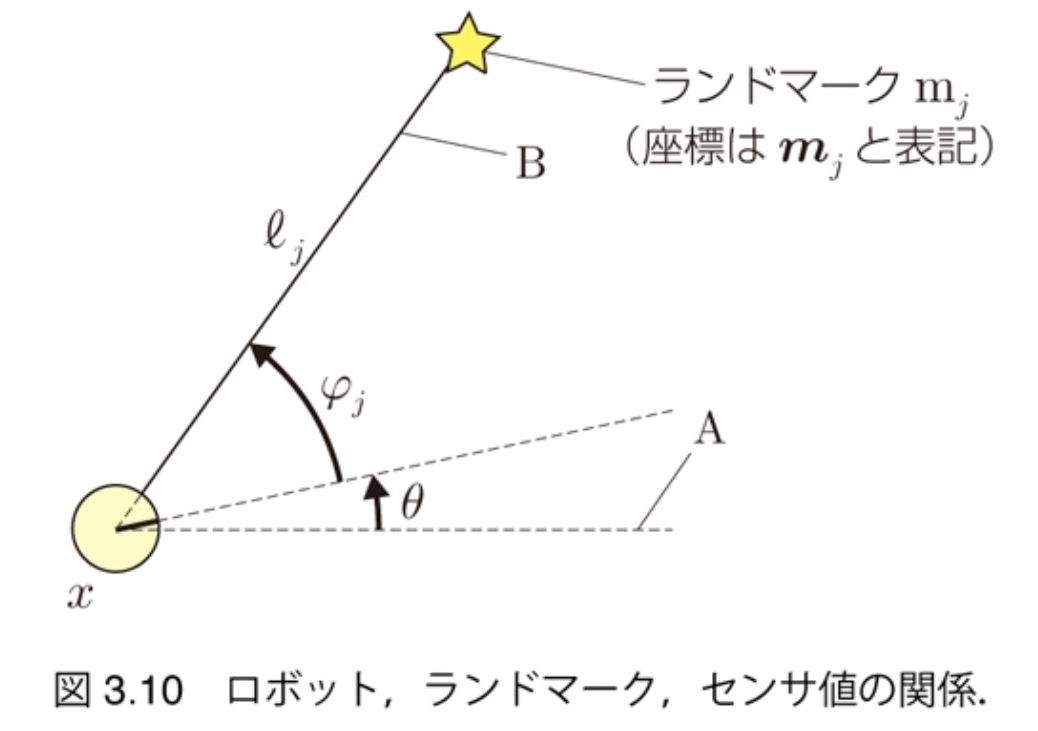
観測方程式
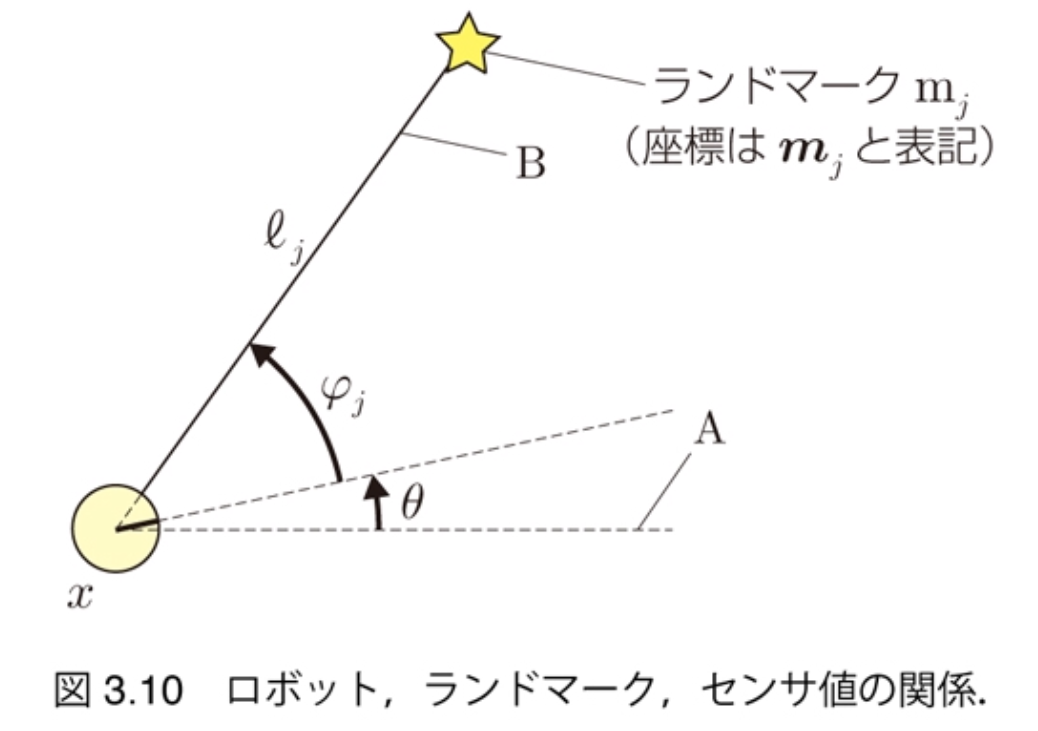
$$ \begin{pmatrix} \ell_j \\ \varphi_j \end{pmatrix} = \begin{pmatrix} \sqrt{(m_{j,x} - x)^2 + (m_{j,y} - y)^2} \\ \text{atan2}(m_{j,y} - y, m_{j,x} - x) - \theta \end{pmatrix} $$
- $z_j = h_j (x)$
- $z_j = h(x, m_j)$(ランドマークの位置を変数とする場合)
- 関数$h_j$: 観測関数
参考代码
class IdealCamera:
def __init__(self, env_map, \
distance_range=(0.5, 6.0),
direction_range=(-math.pi/3, math.pi/3)):
self.map = env_map
self.lastdata = []
self.distance_range = distance_range
self.direction_range = direction_range
def visible(self, polarpos):
if polarpos is None:
return False
return self.distance_range[0] <= polarpos[0] <= self.distance_range[1] \
and self.direction_range[0] <= polarpos[1] <=self.direction_range[1]
def data(self, cam_pose):
observed = []
for lm in self.map.landmarks:
z = self.observation_function(cam_pose, lm.pose)
if self.visible(z):
observed.append( (z, lm.id) )
self.lastdata = observed
return observed
@classmethod
def observation_function(cls, cam_pose, obj_pose):
diff = obj_pose - cam_pose[0:2]
phi = math.atan2(diff[1], diff[0]) - cam_pose[2]
while phi>=np.pi: phi -= 2*np.pi
while phi<-np.pi: phi += 2*np.pi
return np.array( [np.hypot(*diff), phi] ).T
def draw(self, ax, elems, cam_pose):
for obs in self.lastdata:
x, y, theta = cam_pose
distance, direction = obs[0][0], obs[0][1]
lx = x + distance * math.cos(direction + theta)
ly = y + distance * math.sin(direction + theta)
elems += ax.plot([x, lx], [y, ly], color = "pink")
Archives
2019/03 (14) 2020/08 (1) 2021/01 (2) 2021/05 (2) 2021/12 (2) 2022/03 (2) 2022/04 (2) 2023/12 (2) 2024/01 (5) 2024/04 (1) 2024/05 (1)Tags
Recent Posts